Factor analysis
What is factor analysis?
Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. For example, it is possible that variations in six observed variables mainly reflect the variations in two unobserved (underlying) variables.
Factor analysis searches for such joint variations in response to unobserved latent variables. The observed variables are modelled as linear combinations of the potential factors, plus “error” terms. Factor analysis aims to find independent latent variables.
Basic factor analysis illustration
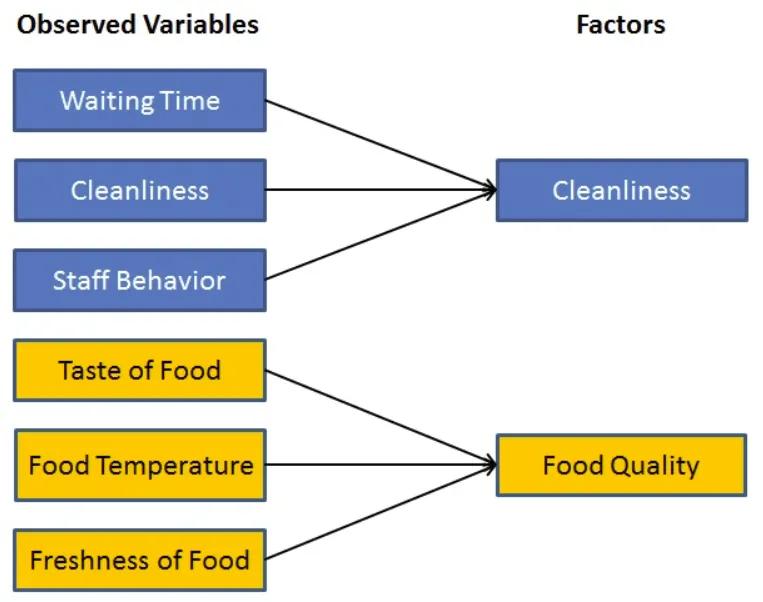
Source: DataCamp
Factor analysis is a way to take a mass of data–or multiple variables–and shrinking it to a smaller number of variables that are more manageable and more understandable. More technically, running a factor analysis is the mathematical equivalent of asking a statistically savvy oracle the following: “Suppose there are N latent variables that are influencing people’s choices. Tell me how much each variable influences the responses for each item that I see, assuming that there is measurement error on everything”. Often the behavior or responses that are being analyzed comes in the form of how people answer questions on surveys.
Factor analysis aims to give insight into the latent variables that are behind people’s behavior and the choices that they make. Principal Component Analysis (PCA), on the other hand, is all about the most compact representation of a dataset by picking dimensions that capture the most variance. This distinction can be subtle, but one notable difference is that PCA assumes no error of measurement or noise in the data; all of the noise is folded into the variance capturing.
Implementing factor analysis
Several factor analysis libraries and packages are available to data scientists, including:
- Factor analysis in R is available with the “Psych” package
- FactorAnalysis in sklearn (sklearn.decomposition.FactorAnalysis) is a Python option
- The “factor_analyzer” package is another Python option


