Overfitting
What is Overfitting in Machine Learning?
Overfitting describes the phenomenon in which a model becomes too sensitive to the noise in its training set, leading it to not generalize, or to generalize poorly, to new and previously unseen data. As an example, a polynomial regression model or a deep neural network may be overtrained to fit too closely the variance in a dataset that possesses merely a linear relationship between input and target variables.
Because this noise has been errantly captured by the model, it will exhibit erratic, nonlinear behavior when it predicts on new data samples manifesting that same linear relationship. In a business context, overfitting can lead to complex models which generate spurious predictions that have a negative impact on model and business performance.
Why is my Model Overfitting?
Overfitting can happen when a model is overparameterized, when it is left to train for too long, or when regularization is not adequately utilized. It can also happen when there are insufficiently few examples in the training set, or when the training set is unbalanced. While a simple model may underfit on a small dataset, a complex model will likely overfit in that same scenario as it will likely be able to capture the relationship in the small training perfectly. However, this is not desirable, as there will not be enough information encoded in the training set as to the true relationship between variables in the underlying data distribution, so the model will end up overfitting to noise.
For unbalanced classification data, an overfit model may learn that it is optimal to simply always predict the dominant class, even though this does not capture the nuance of the data whatsoever. Likewise, this reasoning can be extended to overparameterized models on larger training sets. Even if a training set is on the larger side, if a model has high complexity, such as a neural network with millions or billions of parameters, then it will still be able to fit the random noise in the data.
The same can happen if a model is left to train for too long. In the early stages of training, most optimization steps lead to large jumps in performance related to high magnitude gradient signals and capturing true relationships in the underlying data. However, after some training time as past, most of this signal has already been sufficiently captured and further incremental benefits tend to come from fitting noise in the dataset, even though this is not beneficial for downstream generalization. Finally, regularization is one of the key techniques for combatting overfitting, and when it is underutilized overfitting often occurs.
What Happens if Your Model Experiences Overfitting?
Models are trained on training data, for which the labels are already available. Obviously, this is not the same data that the models will see in production, for if it was there would be no need to train a model in the first place! When an overfit model encounters data outside the training distribution, it will generalize poorly. This means it will generate incorrect predictions, which can lead to devastating consequences in a business setting.
For example, a fraud detection model that is overfit to a training dataset with a large number of fraudulent credit card transactions may start to predict that nearly every credit card transaction is fraud, leading perhaps hundreds of thousands, or even millions, of paying customers to have their transactions declined. In order to remedy this, it’s important to reduce the amount of variance that a model is capturing without going too far in the wrong direction and introducing significant bias. Doing so is a delicate balance codified in a concept called the bias-variance tradeoff.
The Bias-Variance Tradeoff
Bias and variance are two sides of the same coin. When one turns up a model’s variance, its bias goes down, and vice versa. Variance refers to a model’s ability to capture arbitrary relationships in data, while bias reflects the structural strength of a model, or how closely it adheres to a modeling hypothesis. Strongly biased models will learn strictly codified relationships such as purely linear dependencies, whereas high variance models will flex relative to the data that’s thrown at them. Some flexion is good—after all, the ultimate goal of machine learning is to learn relationships from data.
However, too much can be counter to what’s beneficial. Every model requires at least some degree of encoded prior belief about the data in order to be useful. A helpful way to think about this is that a model which can learn anything actually learns nothing. Overfit models exemplify this maxim. They might “learn” anything about the training data you throw at them, perhaps even achieving 100% accuracy on the training set, but when you throw unseen data at them, they will fail in spectacular ways.
How to Address Overfit Models
Overfitting can be addressed in a variety of ways. Perhaps the easiest way to address overfitting is to alter your training data. If your training dataset is small, you should try to gather more training examples. Doing so will almost surely reduce the amount of overfitting that a model is exhibiting. Similarly, if your data is unbalanced, you should try to balance it by adding examples from the underrepresented class, or by applying techniques such as SMOTE, oversampling, undersampling, or bagging, all of which reduce the effect of data imbalance.
Feature selection is another tool that can be used to help alleviate overfitting. Normally, models overfit when they have too many features. Analyzing the mutual information or correlation between features and model outputs, using explainable models such as decision trees, and applying procedures such as forward feature addition or recursive feature elimination can remove unneeded or harmful features while retaining the ones that are most important to achieving good predictive results.
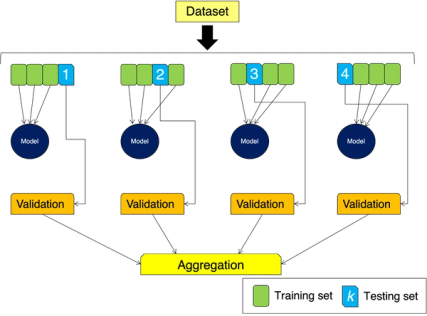
Performing cross validation is also important for addressing overfitting in models. In k-fold cross validation, the training set is divided into k, evenly-sized partitions. In each stage of the process, (k-1) of these are used to train on and the kth remaining one is used for evaluation. By iteratively training across (and evaluating on) different partitions of the data, the tendency of the model to overfit to any one part is reduced. Finally, perhaps the most important and practical way of reducing overfitting is via ensembling and regularization. In ensembling, many models are trained on the same training set, and then their individual predictions are averaged or voted on to arrive at the final, overall prediction. Because different model types learn different biases and different degrees of variance, ensembling helps to reduce the effect of any one model’s overfitting.
Regularization, on the other hand, reduces the variance of a model by constraining its weights. Regularization is most commonly imposed via the addition of a penalty term to the training loss function corresponding to the value of some norm of a model’s weights. By restricting the magnitude attainable by a model’s weights, the model is forced to learn the same relationships in the data using less modeling power, thereby limiting its variance. Other techniques such as dropout applied to neural network weights have also shown to exhibit a regularizing effect.